專欄文章

      本文要介紹的是HodgeRank，一個基於比較數據來建構的推薦系統 [1]；本文將簡單介紹何謂推薦系統（Recommendation System），再接著說明何謂配對比較數據（Pairwise Comparison Data），最後將簡介 HodgeRank 為何，及其應用的各種場景。

      首先，推薦系統是一個訊息過濾系統，用於預測出使用者們對於相異物件之間喜好程度（Preference）的系統。推薦系統做為一個研究領域，旨在研究如何將透過使用者對於部分物件的已知喜好程度，來推論該使用者對於其他未知物件的喜好程度。

      推薦系統被廣泛應用在大量領域中，如：購物網站的廣告欄、YouTube 中的推薦影片或音樂清單、搜尋引擎的搜尋結果排序和 Netflix 的推薦清單等等，在這些由企業針對使用者進行有效的訊息推送的過程中，就是推薦系統最常見的應用場景；廣泛而言，只要使用者有需要找到什麼特定物件，或是比較相似物件時，技術上都是經由推薦系統在背後運作，進而協助使用者來解決問題。

      接著，我們來討論何謂配對比較數據，配對比較數據指的是資料是以使用者對於兩相異物件之間的喜好程度來記錄（對單一物件可能沒有明顯的明確的喜好程度）。一般而言，人很難直接排列出超過10個相異物件的喜好程度 [2]，但我們可以發現，人很容易比較兩相異物件之間的喜好程度；實際上，在現實世界中，相較於物件之間的直接喜好排序，資料往往更容易以配對比較數據呈現在生活中，舉例來說，球隊的排名通常難以直接決定，但我們可透過球隊倆倆之間的競賽結果（如：勝場次、比數差、累積分數差等）來獲得配對比較數據。

      但是不同的配對比較數據，可能會導致出矛盾的結果，例如：A物件比B物件好1分，B物件比C物件好1分，但C物件也比A物件好1分，在這樣的情況下，使用者對於任意兩相異物件都有喜好之分，但是這A、B、C三個物件中，並沒有一個喜好度最高的物件，在實際生活中，配對比較數據無法給予單一物件的喜好排名的狀況經常有之，例如：火影忍者中被遺忘的屬性相剋關係圖，就是一個沒有絕對強弱之分的狀況，見圖一。

                                                                                                          

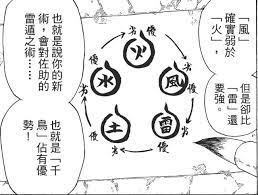
                                                                                                        圖一：火影忍者中的忍術屬性關係圖（擷取自網路）

      上述例子中，由於三個物件彼此之間的喜好差異是一樣的，在這種情況下，若我們仍然希望給使用者這三物件之間的喜好排序，一個較為合理的推薦系統，其推薦結果必然是三者的喜好程度都一樣（否則對於任一個物件都會”不公平”），因此，HodgeRank 便是如何將配對比較數據上轉換成所有物件之間喜好排序的一個推薦系統演算法。

 

      然後，我們來簡介何謂HodgeRank，如上所述，HodgeRank 便是用來將物件之間的配對比較數據上轉換成所有物件的喜好排序的一個演算法，該演算法的基本原理是嘗試將各物件指派一個喜好分數（Preference Score），並希望相異物件之間的喜好分數的差距，恰巧是已知的配對比較數據的值，換言之，假設使用者對於物件 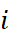  的喜好程度高於物件  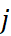，且其喜好差異為 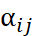，若兩個物件之間的喜好分數分別為  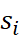與 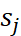  ，則我們希望

                                                                                                

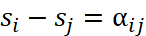
      如此一來，該喜好分數 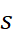   便能相容於物件  與物件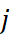  之間的比較配對數據 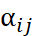，但由於配對比較數據不僅一組，所以我們希望  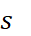能盡可能的相容魚所有的配對比較數據，因此，我們可以考慮下面的最佳化問題：

      若有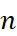  相異物件 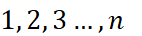  ，一組配對比較數據可表示成一個斜對稱函數  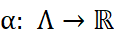，其中 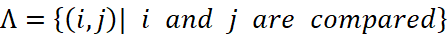 代表的所有被配對比較過的物件組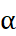；  是斜對稱函數表示  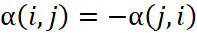 。為了方便起見，我們將 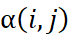 寫作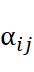 。為了找出一相容於配對比較數據的喜好分數，我們考慮下面的最小平方問題：

                                                                                              

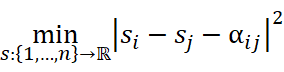
其中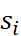，  代表的是 。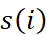

 

       值得注意的是，這個最小平方問題的解函數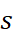  並不唯一，因此，我們要考慮所有的解當中，其總和為0的，亦即 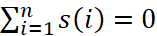，在[1]當中，作者們由圖論的角度出發，將上述最佳問題轉換成一與圖拉普拉斯矩陣（Graph Laplacian）相關的問題，此外，透過組合Hodge理論，總和為0的最小平方解的存在性是成立的，並可透過計算圖拉普拉斯矩陣的廣義逆矩陣（Generalized Inverse）來求解計算，由該方法所計算出的最小平方解 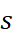，就稱之為配對比較數據的HodgeRank，由於篇幅因素，就不另外討論 HodgeRank 背後的數學理論及演算法。

 

      在本文最後，我們來介紹這樣的配對比較數據應用在哪些領域。在影片品質評估（Video Quality Assessment）上，HodgeRank 的作者們透過HodgeRank將不同影片的透過品質進行分類 [3]。在兩兩競賽的運動競賽中，[4] 應用了 HodgeRank 來給出一個較為合理的競賽成績排名；筆者與博士班指導教授，則將 HodgeRank 應用在同儕互評（Peer Assessment）中，藉此消除同儕互評中的各種偏差性，並提供了授課老師如何將同儕互評的成績轉換成絕對分數的一種參考 [5]。

 

撰文者：政大人工智慧與數位教育中心   林澤佑研究員

---

參考文獻：

1. Jiang, X., Lim, L. H., Yao, Y., & Ye, Y. (2011). Statistical ranking and combinatorial Hodge theory. Mathematical Programming, 127(1), 203-244.
2. Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological review, 63(2), 81.
3. Xu, Q., Huang, Q., Jiang, T., Yan, B., Lin, W., & Yao, Y. (2012). HodgeRank on random graphs for subjective video quality assessment. IEEE Transactions on Multimedia, 14(3), 844-857.
4. Sizemore, R. K. (2013). HodgeRank: Applying combinatorial Hodge theory to sports ranking (Doctoral dissertation, Wake Forest University).
5. Lin, T. Y., & Tsai, Y. L. (2018). An Application of HodgeRank to Online Peer Assessment. arXiv preprint arXiv:1803.02509.