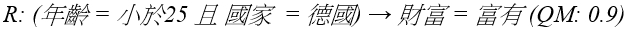子群組探勘(Subgroup Discovery)簡介
【從描述性探勘、預測性探勘到子群組探勘】
在人工智慧資料探勘領域中,處理分類、迴歸問題的「預測性探勘」(predictive induction)和以案例的特徵變項歸納出可能分類的「描述性探勘」(descriptive induction)是爲人所知的兩大主流類型(Kantardzic, 2011)。而「子群組探勘」(subgroup discovery)則是介於兩者之間,讓資料分析者探勘造成特定現象可能原因的一種方法。
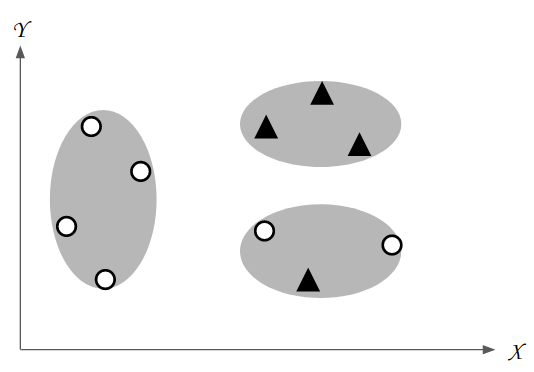
首先,先讓我們來回顧描述性探勘的特性。描述性探勘是在研究者尚無特定假設或欲關注的現象時,為尚未釐清的資料歸納背後隱含規則的一種方法。描述性探勘所使用的演算法又稱之爲非監督式機器學習演算法(unsupervised machine learning algorithm)。圖一是描述性探勘結果的示意圖。根據各個案例在變項x與變項y兩種特徵的相似程度,描述性探勘可以將這10個案例分成3群。然而,實務上資料分析的任務大多會存在既定的假設,就像圖一的案例可分為▲或O兩種類型,但描述性探勘在找尋案例之間的關係時並不會全然關注這兩種類型,導致分群結果往往並不能有效區分案例▲和案例O,也就很難將分群結果視為造成案例▲和案例O的可能原因。
|
圖一、 描述性探勘結果示意圖 |
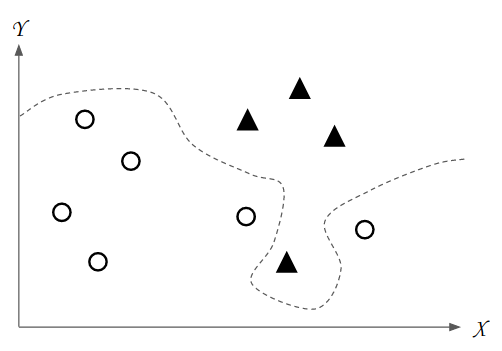
另一方面,如果資料分析者已經抱持著特定的假設或目標,需要建立各個案例的特徵與該目標之間的規則時,那就非預測性探勘莫屬。預測性探勘採用的演算法稱爲監督式機器學習演算法(supervised machine learning algorithm),意味著資料本身已經有既定的規範和目標,而演算法則是要針對該目標建立可預測的規則。這些規則又稱之爲模型(model)。圖 2係預測性探勘的分析結果示意圖。圖中的虛線將兩種不同的案例▲或 O明確分開,這也就是預測性探勘所歸納出的模型。當未來出現了新的案例時,資料分析者可依照此模型來判斷該案例屬於▲還是O,以此完成預測性探勘的任務。不過,爲了使預測結果達到近乎完美的準確,現今預測性探勘所採用的深度學習(deep learning)演算法,往往建構出人們無法理解的黑箱模型(black box model)。以圖二爲例,我們很難說明虛線彎曲的規則,而實務上的黑箱模型則是更加的複雜。
|
圖二、預測性探勘結果示意圖 |
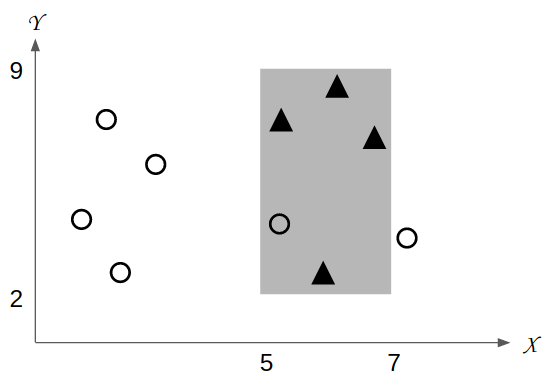
為了克服預測性探勘和描述性探勘各自的限制,越來越多研究者將監督式和非監督式機器學習演算法各自的優點彼此結合,發展出了資料探勘中第三種類型的分析技術:子群組探勘(subgroup discovery)。子群組探勘類似於預測性探勘,資料分析者一樣都有欲聚焦的特定目標,但比起預測性探勘追求正確的分類和預測,子群組探勘則更著重於歸納人類能夠理解、應用的規則。圖 3是子群組探勘結果的示意圖。資料分析者若要歸納出現案例▲的可能規則,便可利用子群組探勘找出多個不同的「子群組」(subgroup)。子群組包含了造成該子群組的前提條件,以及用來表示值得資料分析者關注的品質評估指標。子群組探勘將依據品質評估指標由高到低選出品質最好的子群組作爲最後結果。圖三中灰色區域是子群組探勘所找出的其中一個子群組。灰色區域反映了變項x與變項y在一定區間的範圍,而該範圍中的案例▲比例明顯較多。在全部10個案例中,案例▲僅佔了40%。但若將灰色區域納入考慮之後,會發現灰色區域中的4個案例裡,案例▲就佔了80%。由此可知,灰色區域可能是造成更多案例▲的原因之一,值得資料分析者特別注意。
|
圖三、子群組探勘結果示意圖 |
比較圖二和圖三之間的差異,可以很容易瞭解子群組探勘與預測性探勘之間的不同。子群組探勘所歸納的子群組並非以正確率爲優先目標,而是著重於歸納出統一且容易解釋的規則。圖三的灰色區域並沒有將案例▲和案例O完全分離,但卻能夠得到容易解釋的規則。從子群組「特徵變項x介於8到12之間、且特徵變項y介於5到9之間的案例,有80%會是▲」的規則裡,資料分析者可輕易地與自身的領域知識相互結合,歸納出合理的解釋。由於子群組探勘所找出的規則容易理解,因此可視為是一種白箱模型(white box model)。利用子群組探勘所發掘的規則與領域專家的知識相互結合,將可協助資料分析者發掘在資料背後的隱含知識。
【子群組探勘之子群組】
子群組探勘的目標是發掘最值得資料分析者關注的子群組(subgroup),接著就讓我們來認識一下子群組的詳細定義。子群組係由描述變項(descriptive attribute)及其範圍(scope)所構成的前提條件(condition)、該前提條件下涵蓋的案例(instance)之目標變項(target attribute)及其區間(interval),以及將子群組值得資料分析者關注的程度進行量化計算後得到的品質評估指標(quality measure)。
|
式一 |
式一的子群組 R 呈現了子群組中的前提條件、目標變項以及品質評估指標。Cond(Descriptivevalue)係指該子群組的前提條件。符合此前提條件的案例,將被視為子群組所涵蓋的案例。Targetvalue係指子群組探勘中研究者所感興趣的目標變項及其區間。QM係指該子群組的品質評估指標。QM越高,表示該子群組越值得資料分析者關注。
以下用Herrera等人(2011)所舉的例子來說明子群組的描述方式。給定 D 為資料集,資料集中包含了大量案例。這些案例具備了四個特徵變項,其中三個為描述變項,最後一個為目標變項。描述變項的名稱與值域各別為「年齡={小於25,25到60,大於60}」、「性別={男性,女性}」、「國家={西班牙、美國、法國、德國}」。而資料分析者關注的目標變項其名稱與值域為「財產={貧窮,普通,富有}」。資料分析者以此資料集選定欲關注的現象,例如「財富=富有」,即可利用子群組探勘發掘多個子群組。式二為其中一個子群組的例子:
|
式二 |
在式二的子群組R中,前提條件是年齡小於25歲的德國人,其品質評估指標為0.9。由此可知,年紀較輕的德國人可能是成為有錢人的原因之一,值得資料分析者關注。
【子群組探勘實際範例】
實作了子群組探勘演算法的工具已經十分成熟,而且大部分工具都可在不同作業系統中使用。以下我們就以Duivesteijn等人(2016)所發展的Cortana作為例子,為讀者展示子群組探勘的實際運作過程。Cortana是以Java開發的應用程式,因此Linux、Mac和Windows等作業系統的使用者可直接使用。Cortana的特別之處在於實作了特殊模型探勘演算法(Exceptional Model Mining, EMM)。特殊模型探勘將傳統子群組探勘的目標變項拓展成目標概念(target concept)。目標概念不僅可以相容於類別變項的目標變項,還能夠處理連續數值類型或多個目標變項。隨著目標概念的類型不同,特殊模型探勘發展許多相對應的品質評估指標。以下本文將以常見的單一連續變項的目標概念作為例子,讓讀者瞭解以Cortana進行子群組探勘的實例。
|
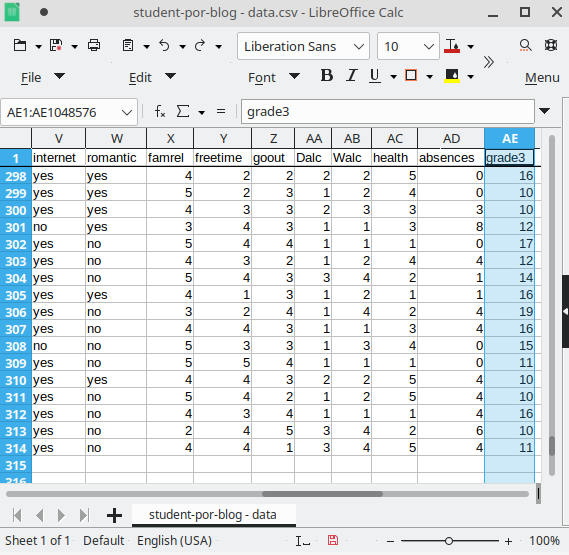
圖四、學生學習表現資料集 |
本文準備了來自UCI機器學習保存庫(UCI Machine Learning Repository)的學生學習表現資料集(Student Performance Data set) (Cortez & Silva, 2008)作為例子。該資料集是學校校務系統常見的資料形式,如圖四所示,它包含了學生的個人資訊(就讀學校、性別、年齡、住處)、父母(教育、職業)、學習支援(來自學校、來自家庭)、補充課程(補習)、學校表現(犯錯次數、缺席次數)以及學期成績。為了便於說明,本文將該資料集稍作調整。教師所聚焦的目標變項即是最後一個特徵grade3,代表學生最後的學期成績。而究竟是怎樣的規則可能導致學生的學期成績較高呢,以下我們就用Cortana進行子群組探勘,幫教師找出可能的原因吧。
|
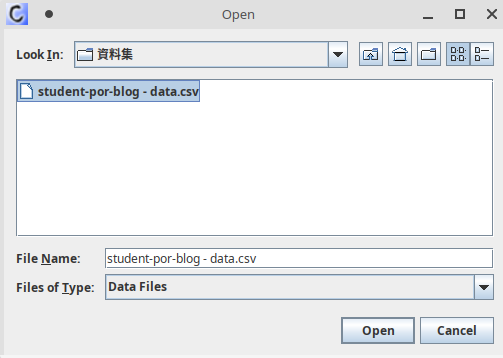
圖五、Cortana選擇檔案 |
Cortana開啟後第一個畫面是選擇檔案,如圖五所示。請選擇剛剛下載的資料集開啟。
|
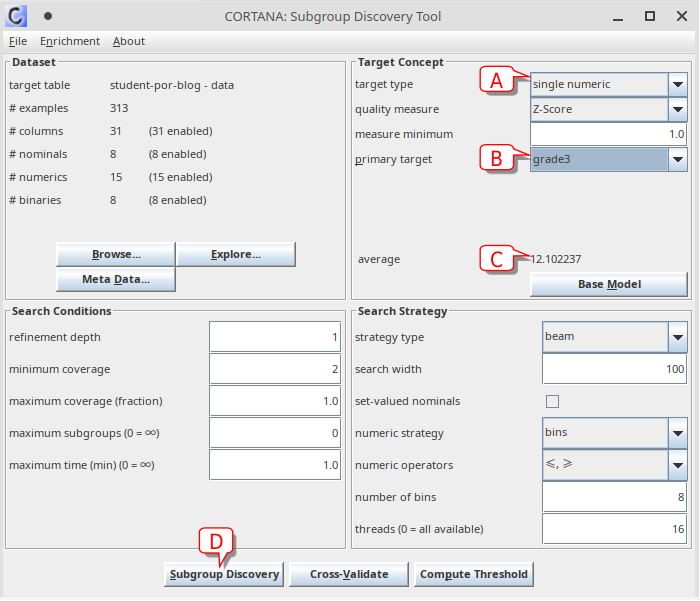
圖六、Cortana主要操作畫面 |
開啟檔案後,即可看到Cortana的主要操作畫面。首先我們要在目標概念裡設定欲關注的現象。請在圖六的Target Concept (目標概念)下找到A處的target type (目標類型),選擇「single numeric」(單一連續變項)。此時下方的quality measure (品質評估指標)也會切換單一連續變項預設的計算方式Z-Score。接著在B處的primary target (主要目標變項)選擇「grade3」,此變項為學生最後的學期成績。在C處會顯示該資料集裡grade3的平均值,也就是整個資料集裡所有學生的平均學期成績為12.1分。再來我們按下D處的Subgroup Discovery (子群組探勘),即可開始進行探勘。
|
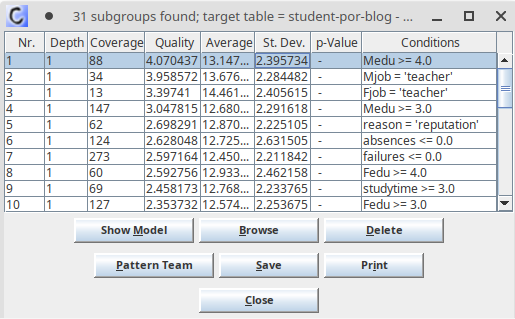
圖七、子群組探勘結果 |
探勘完成後,Cortana列出找到的31個子群組,並以品質評估指標由高到低排序。如圖七所示,表格的8個欄位意義如下:
- Nr.:子群組排序。
- Depth:深度。也就是前提條件的條件數量。
- Coverage:子群組涵蓋案例的數量。
- Quality:品質評估指標。
- Average:平均值。
- St. Dev.:標準差。
- p-Value:該子群組的「特殊」程度。這是特殊模型探勘的演算法內容之一,不過僅有部分類型的目標概念才能計算p-Value,此例子並不適用。
- Conditions:前提條件。由特徵變項與範圍所組成。
從圖七中可以得知,品質評估指標最高的子群組,其前提條件為「Medu >= 4」,意思是學生母親受過高等教育。而該子群組的學期成績平均值為13.14,比整體資料集的平均值12.1還要高。由此可知,學生家長的教育水準,可能會與學生的學習表現有所關聯,值得教師進一步探討其背後的意涵。
然而,光就平均值來看,排序第二個的子群組平均值有13.68,高於第一個子群組,那為什麼會排在第二呢?這是因為我們使用的品質評估指標Z-Score,不僅能夠找出平均值更高的子群組,也同時會將子群組的涵蓋案例數量納入考量。Cortana的Z-Score應用了統計學的標準分數概念,計算方式如式三所示:
|
式三 |
Coverage表示該子群組涵蓋的案例數量;Sum表示子群組的目標變項加總;TotalAvg為整體資料集的目標變項平均值;TotalSampleStd 為整體資料集目標變項的樣本標準差。
在瞭解了品質評估指標Z-Score的計算方式後,讓我們再來回頭看看圖 7中第一個子群組和第二個子群組之間的差別。第一個子群組的平均值為13.14,涵蓋案例數量為88;第二個子群組的平均值為13.68,但涵蓋案例數量僅有34,不到第一個子群組的一半。換句話說,第一個子群組雖然平均值較低,不過由於涵蓋案例數量更多,最後在品質評估指標Z-Score上得到了較高的分數。涵蓋數量更多,表示該子群組的前提規則能夠適用於更多的案例,更具實用性。
【結語】
子群組探勘是介於預測性探勘與描述性探勘中較鮮為人知的一門技術。有趣的是,這卻是許多資料分析者所欲追求的目標。儘管現今人工智慧著重的預測性探勘能帶來高度正確率的預測答案,但人們卻更想知道隱藏在這個答案背後的規則,以及這些規則背後所代表的隱含知識。
儘管子群組探勘和描述性探勘兩者都是以目標變項來建立模型,但兩者在實務應用的場合上卻有相當大的差異。預測性探勘著重的是預測的正確率,而降低了可解釋性,適合用於已經存在成熟的規則、不需要特別去解釋的任務。舉例來說,飛機與車子的圖像分類任務,我們即使不去歸納區分兩者的規則,也可以相信人工智慧所建置的模型。
另一方面,子群組探勘能夠在兼顧可解釋性的前提下,找出正確率較高的規則。因此子群組探勘特別適合用於規則尚未明朗,或是樣本量較少的任務,尤其是涉及人類活動的社會科學領域。以信用卡申請通過與否的任務作為例子來看,銀行除了使用預測性探勘的人工智慧模型來判斷申請者是否通過之外,還可以結合子群組探勘,歸納出容易解釋的可能原因。這些規則可以用於瞭解信用卡的審核上是否帶有偏見,也能夠對審查結果抱有疑問的客戶給出一個合理的解釋。透過預測性探勘與子群組探勘的有機結合,人們將更能接受人工智慧給出的答案,進一步提升人工智慧結果的社會認可度。
本文最後以致力於可解釋性機器學習的研究者Christoph Molnar的觀點作為結尾:「科學的目標是獲取知識,但現今許多問題仍是透過巨量資料集和黑盒機器學習模型來解決。模型本身應該成為知識的來源,而不是只是數據而已。」(Molnar, 2020)以此與所有人工智慧領域的研究者們共勉之。
撰文者:政大人工智慧與數位教育中心 陳勇汀研究員
參考文獻:
1.Cortez, P., & Silva, A. M. G. (2008). Using data mining to predict secondary school student performance. In A. Brito & J. Teixeira (Eds.), Proceedings of 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008) (pp. 5–12). EUROSIS.
2.Duivesteijn, W., Feelders, A. J., & Knobbe, A. (2016). Exceptional Model Mining. Data Mining and Knowledge Discovery, 30(1), 47–98. https://doi.org/10.1007/s10618-015-0403-4
3.Herrera, F., Carmona, C. J., González, P., & del Jesus, M. J. (2011). An overview on subgroup discovery: Foundations and applications. Knowledge and Information Systems, 29(3), 495–525. https://doi.org/10.1007/s10115-010-0356-2
4.Kantardzic, M. (2011). Data mining concepts, models, methods, and algorithms. John Wiley & Sons Inc. http://cmich.idm.oclc.org/login?url=http://lib.myilibrary.com/detail.asp?ID=323974
5.Molnar, C. (2020). Interpretable machine learning: A guide for making black box models explainable.